First Person Shooter | Game Design
Developed a small arena world-like first person shooter set in a post-apocalyptic time where artificially intelligent robots have went off the rails and took over. The player character is a reclusive person who lives in a shack out in the woods away from most of civilization but still pretty close to abandon urban areas. In order to escape the robots that are quickly closing in, the player must quickly collect all 5 spare parts to reassemble the mechanism to open the gate to the external world. Weapons have different types and ranks which the player must have their skill levels leveled up to in order to use. This is done by collecting a part which gives the player a level and 2 skill points to distribute. The distribution of weapons throughout the level differs with each play through making the players experience a little different each time. Enemies will get harder as more parts are collected.
Enemies also employ a custom algorithm of mine that uses a variation of Boids algorithm to coordinate the robots in large groups (like a wolf pack). The result is that larger groupings of bots result in a "surrounding" tactic where bots take turns attacking the player from all sides. This makes it pretty hard for the player to escape especially when they have exhausted their ability to run. The situation can be made worse by the fact that aggro is added as well which makes nearby enemies become more aware of the players presence when a fellow enemy is under attack (essentially being alerted to come to its aid). Packs are easily formed this way and should be avoided.
The game was made in Unity and some assets are royalty free. The cartoon-ish (or retro) effect is also a custom shader I developed using color quantization and sobel edge filters.


Physically-Based Rendering Engine | 3D Graphics
Developed a custom physically-based rendering (PBR) engine using ray-marching techniques on the GPU. This technique uses what is called a "signed-distance field" (aka SDF) to represent the 3D world that is being rendered. Rays are casted out into the world from screen pixels translated to the camera plane (using a semi-accurate mathematical model for the lens which includes adjustable FOV) and "marched" along their trajectories until they collide with something.
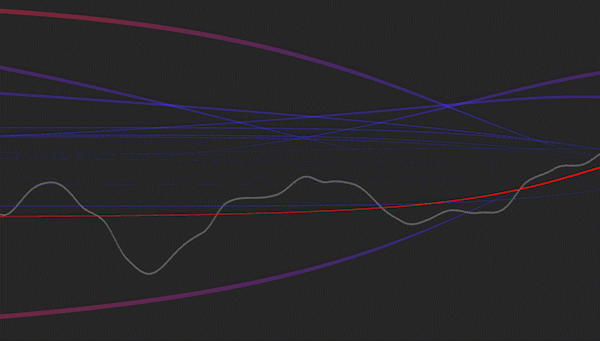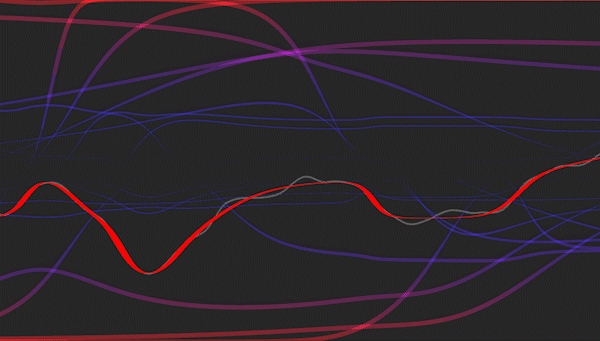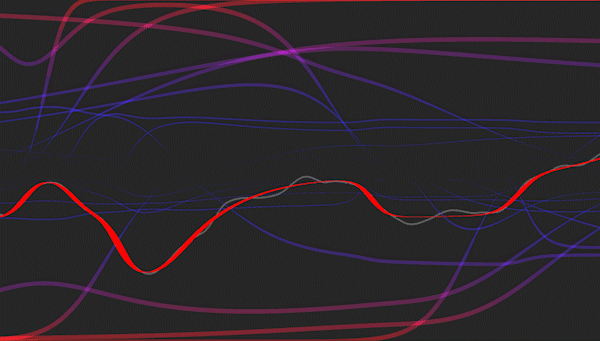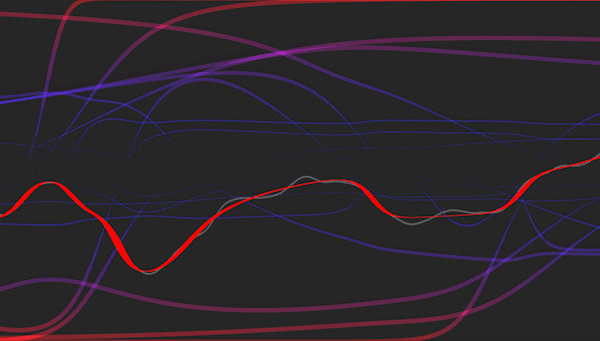
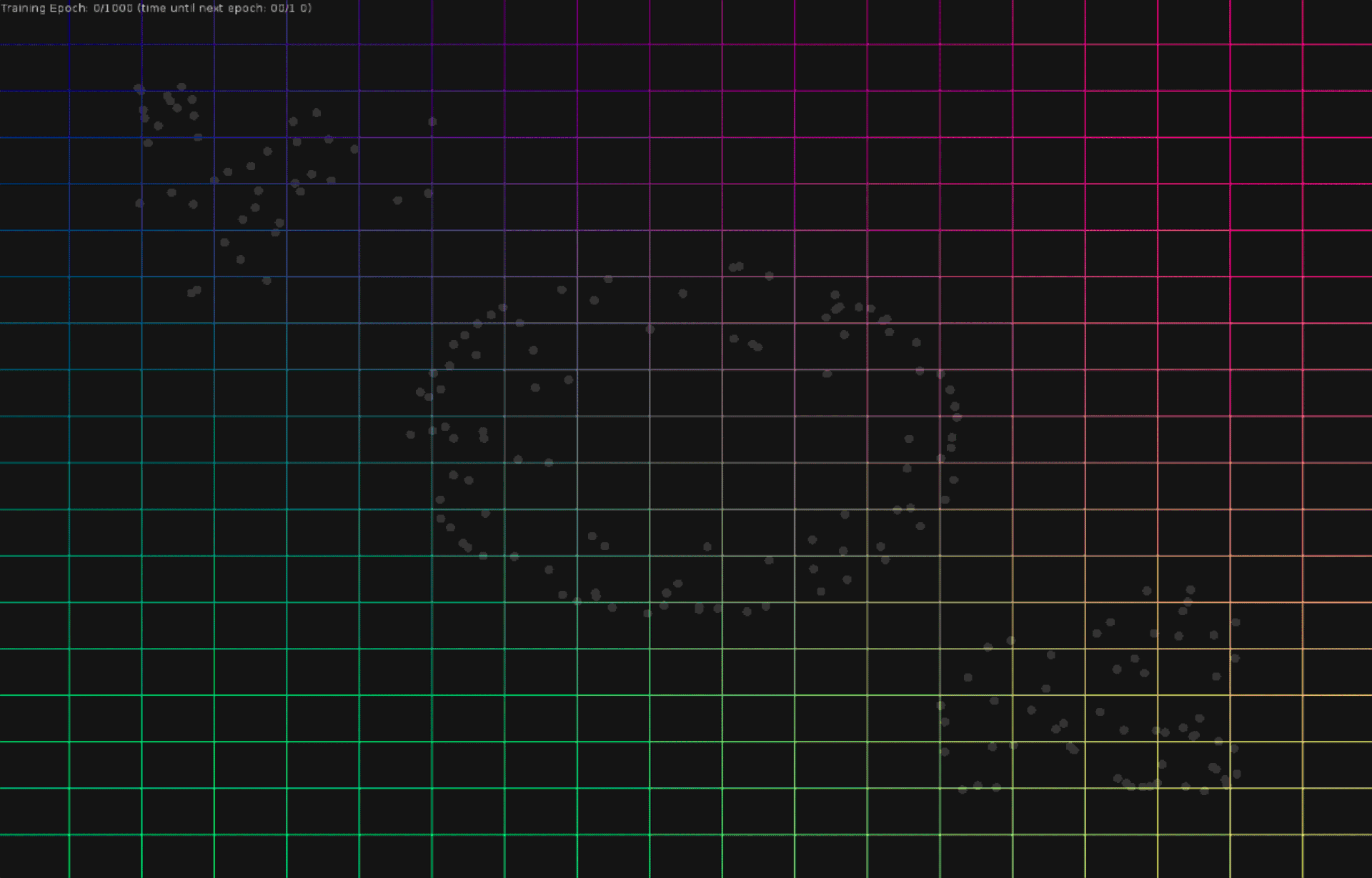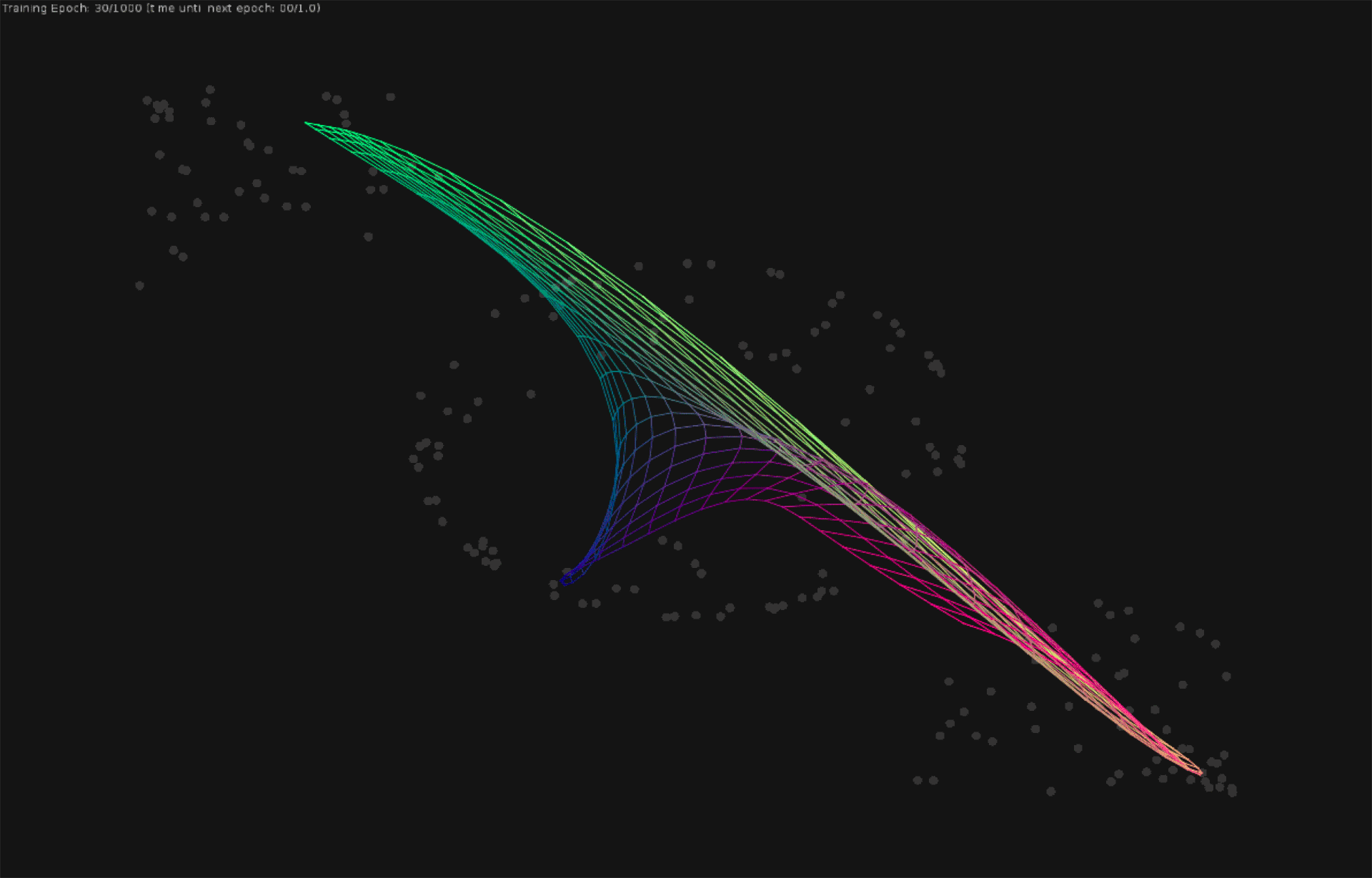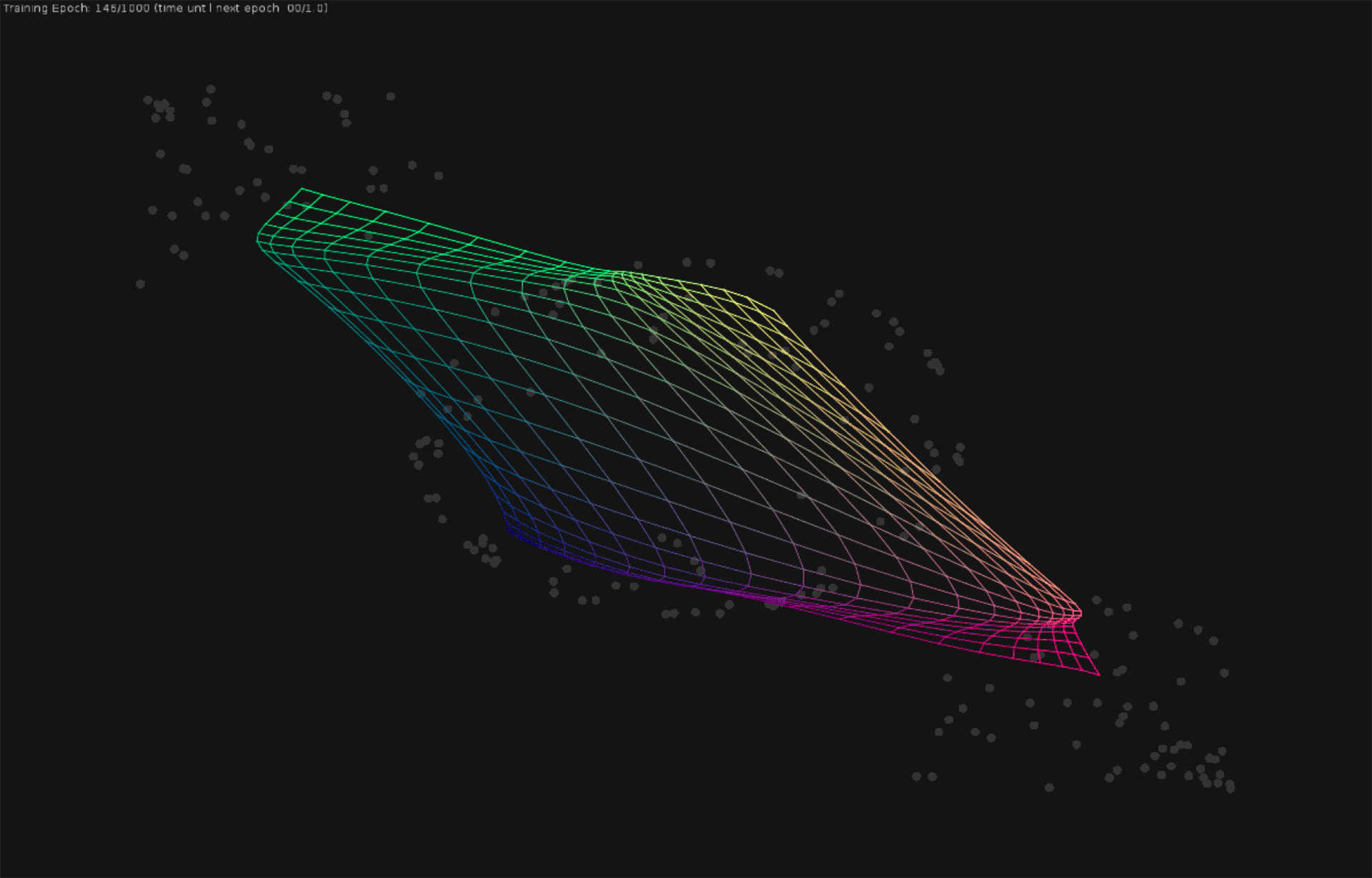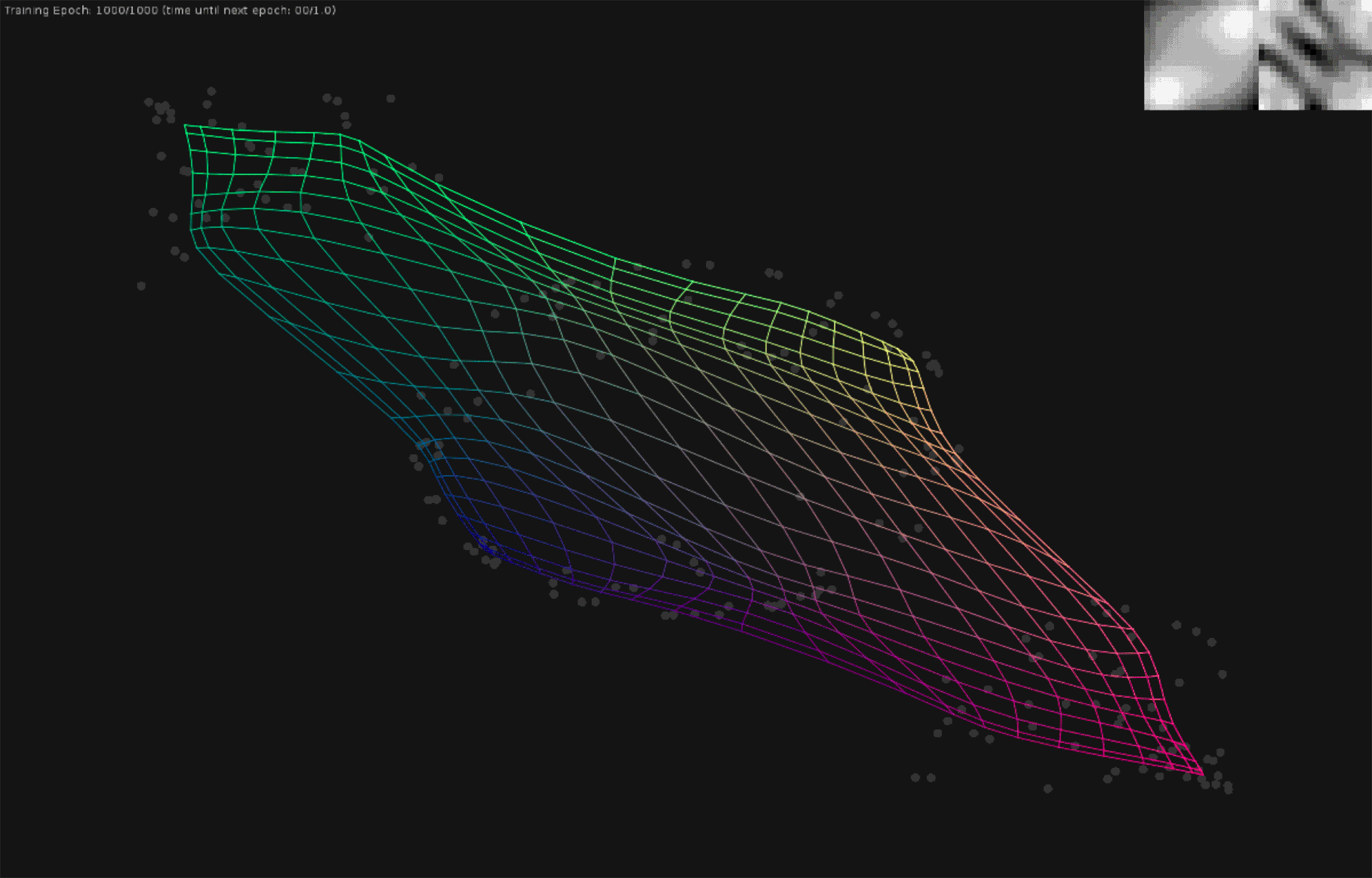
Visualization of a multi-layered perceptron learning a polynomial regression model
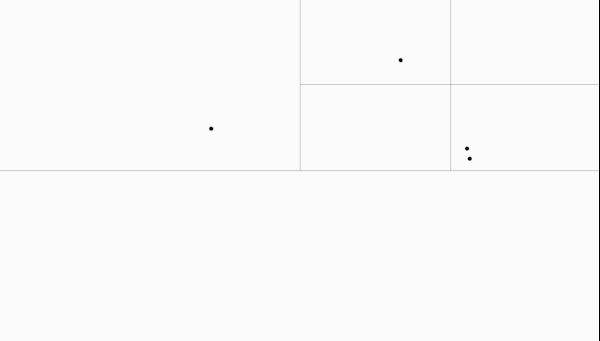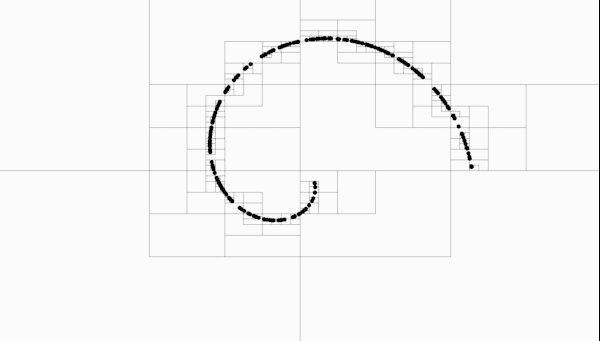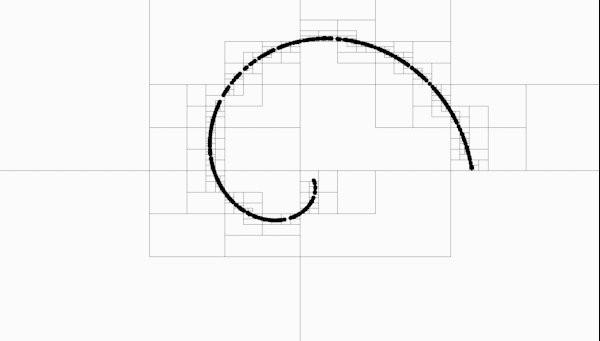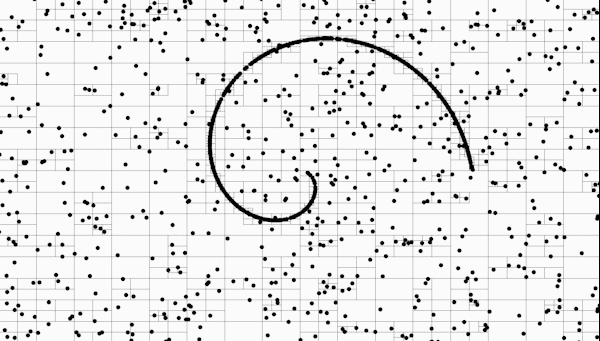
Sparse Quad Tree example on a randomized spiral function
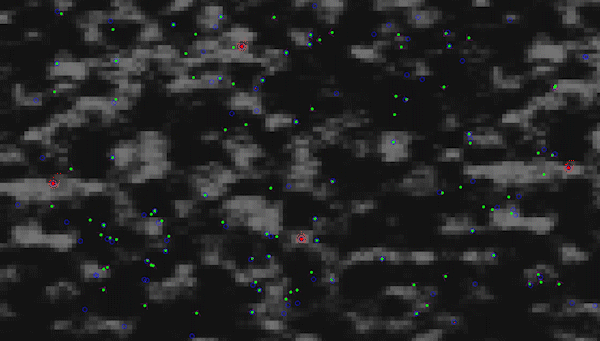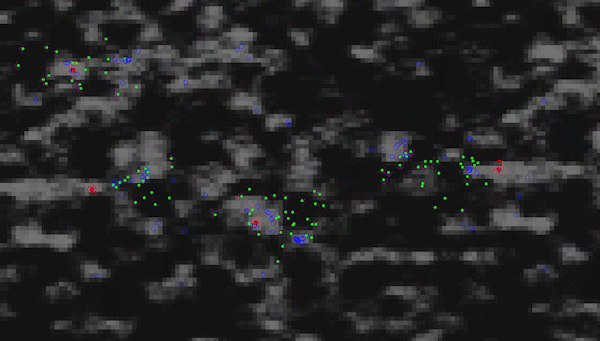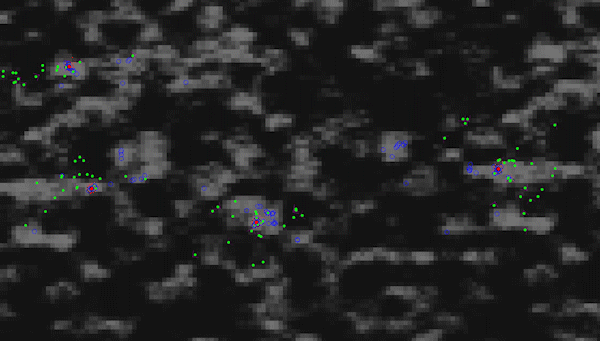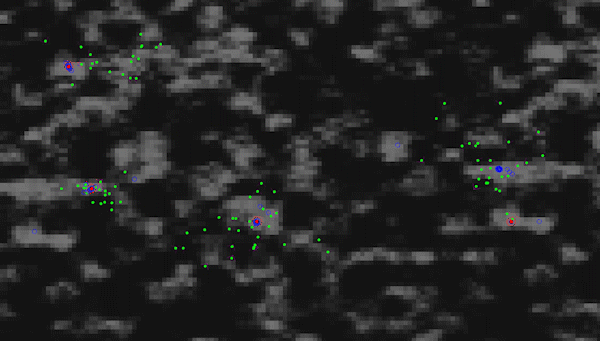
Particle Multi-Swarm Optimization (custom) on a randomized perlin noise function
Some 2018 Projects | Experimental
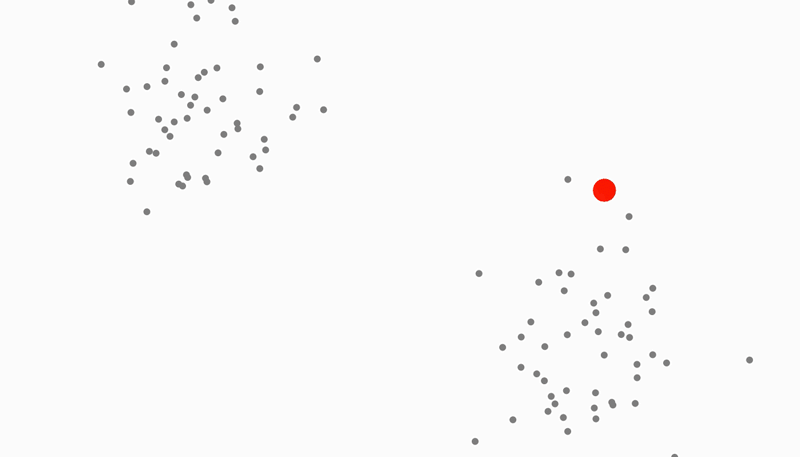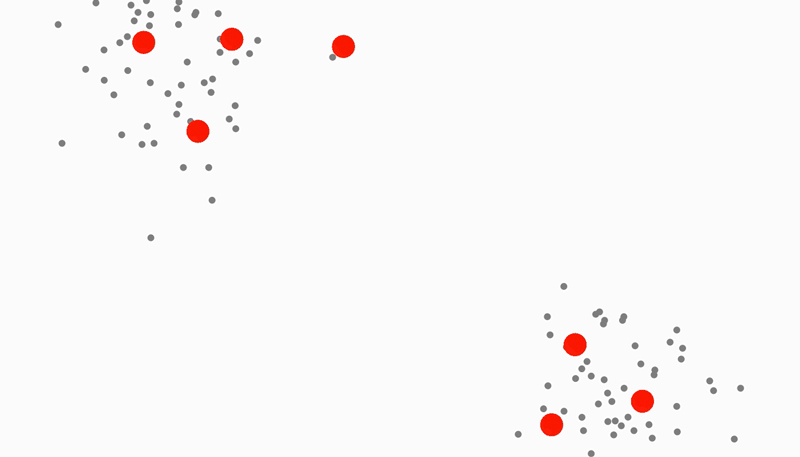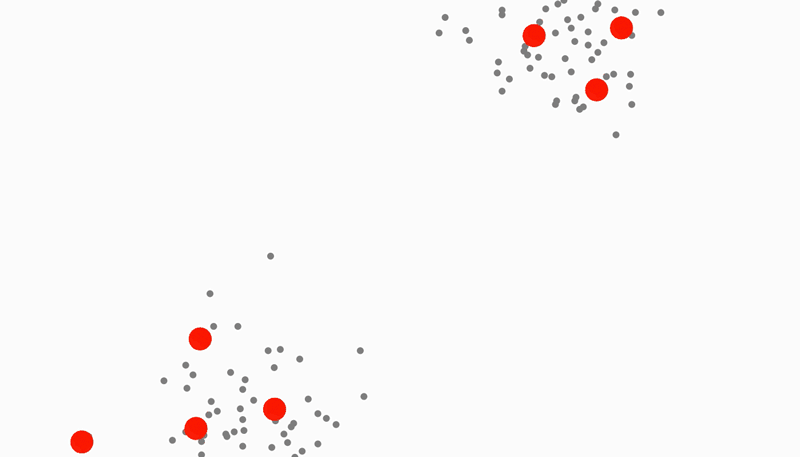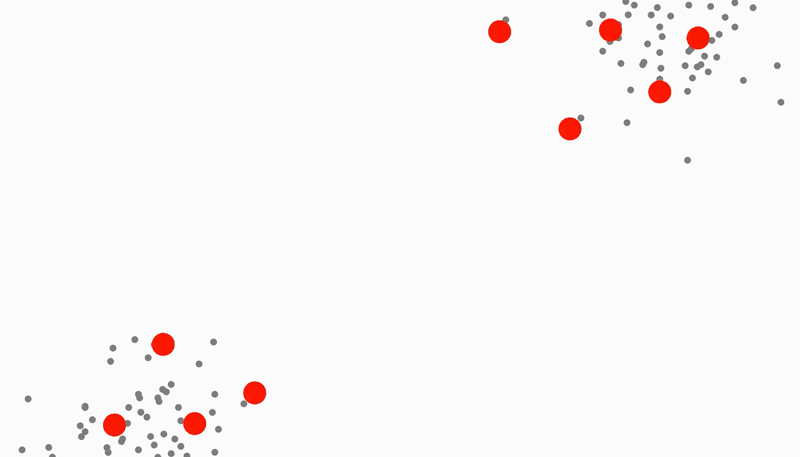
Tracking of clusters without classification

Tracking of clusters with classification
Multi-Tracking K-Means | Motion Tracking
This algorithm was developed on the Microsoft® Kinect for Creatabase, an Art Installation project I lead for Bradley University's Interactive Media exhibition known as FUSE. The project was finished and on display on April 27th, 2018 at the Riverfront Museum in Peoria, IL. Over 300 users participated and even more got to try out the exhibit!
This art installation project was essentially an interactive art gallery where visitors (primarily children) can draw/create pieces of art and have them "digitized" (taken a picture of and uploaded) to a database. This database is then read from and every piece of art in it is rendered on a big projected screen where users can sift through them using their entire bodies. Users movement and distance from the screen will decide whether the art blows around like paper in the wind or comes forward to be expanded and viewed. For this kind of full body interactivity to be a success, an algorithm had to be implemented in order to track multiple users.
The K-Means clustering algorithm is typically used as a way of finding the centers of clusters in a set of data (such as pixels picked up by a camera/sensor for instance). This makes it perfect for finding bodies and other objects. However, standard K-Means requires that the number of clusters to track be specified ahead of time. This was not acceptable in this situation because at any given time there are an unpredictable number of people within view. Thus, I came up with a growing version of the K-Means algorithm that creates new cluster points and removes old ones based on whether they have covered too many or too little points. The result is clusters that appear to be cells performing mitosis in order to cover all the points without getting too close to one another (this distance is also controllable).

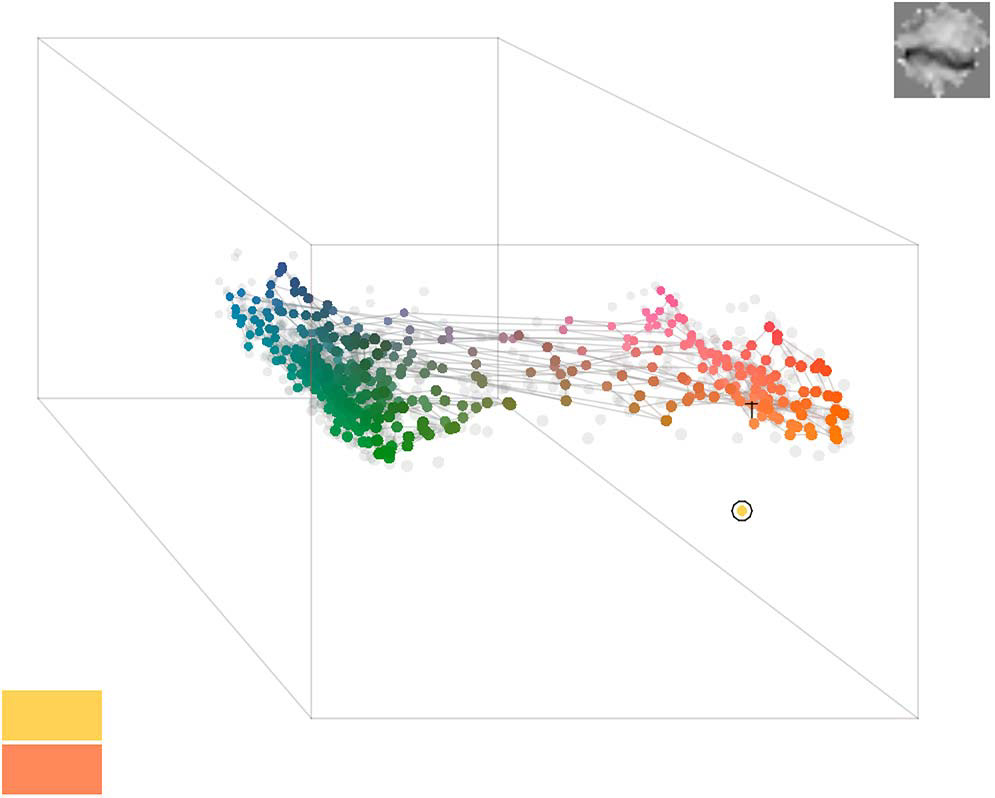
Self-Organizing Map | Machine Learning
Self-Organizing map simulations of a 20x20 feature map. The data sets are a simple 200 to 300 2D data points and 200 to 300 3D color-based data points that have been randomly placed within several cluster spaces. Self-Organizing maps are part of a group of machine learning algorithms known as unsupervised learning and is also defined as a type of neural network. These algorithms focus on learning relationships between input data in order to draw reference to them when presented with new data. Algorithms like these are typically used for data sets that are not already clearly labeled. Self-Organizing maps in particular are often used for reducing the number of inputs by replacing them with nodes that closely represent them (data reduction) and visualizing/organizing data with a high number of dimensions (dimensionality reduction).
The top-right images at the end of the animation is the corresponding U-Matrices mapped as greyscale pixels pertaining to each place (pixel) in the matrix. In a U-Matrix, the pixels greyscale value pertains to the density of that point. In other words, the lighter the value the more clustered neurons/nodes are in that spot in the feature map. Thus, the U-Matrix reveals an always 2D representation of the clusters of data in n-dimensional space. The actual training of the network involves finding the closest neuron (point on the grid otherwise known as a feature on the feature map) and then adjusting every neuron within a certain distance from that point so that they are moved a little closer to it.












2D Trees | Procedural Generation
Procedurally generated 2D trees with texturing and pseudo-lighting. These are some examples produced by an app I developed for the purpose of testing this algorithm. The algorithm uses recursion like most procedural flora but with creative twists like added momentum of growth. The results of the application can vary from erratic to tight and controlled.
The algorithm itself is what is known as a Fractal Tree algorithm where the app starts by making the trunk of the tree followed by splitting the ends of the branch and existing branches into two new branches offset by random angles. As the depth of the tree (amount of splitting) increases, the tree becomes much more complex and possibly self-similar (repeating sequences of self) while zooming in. The trees can also be "seeded" with a sequence to ensure the same tree can be replicated at any time in the future.








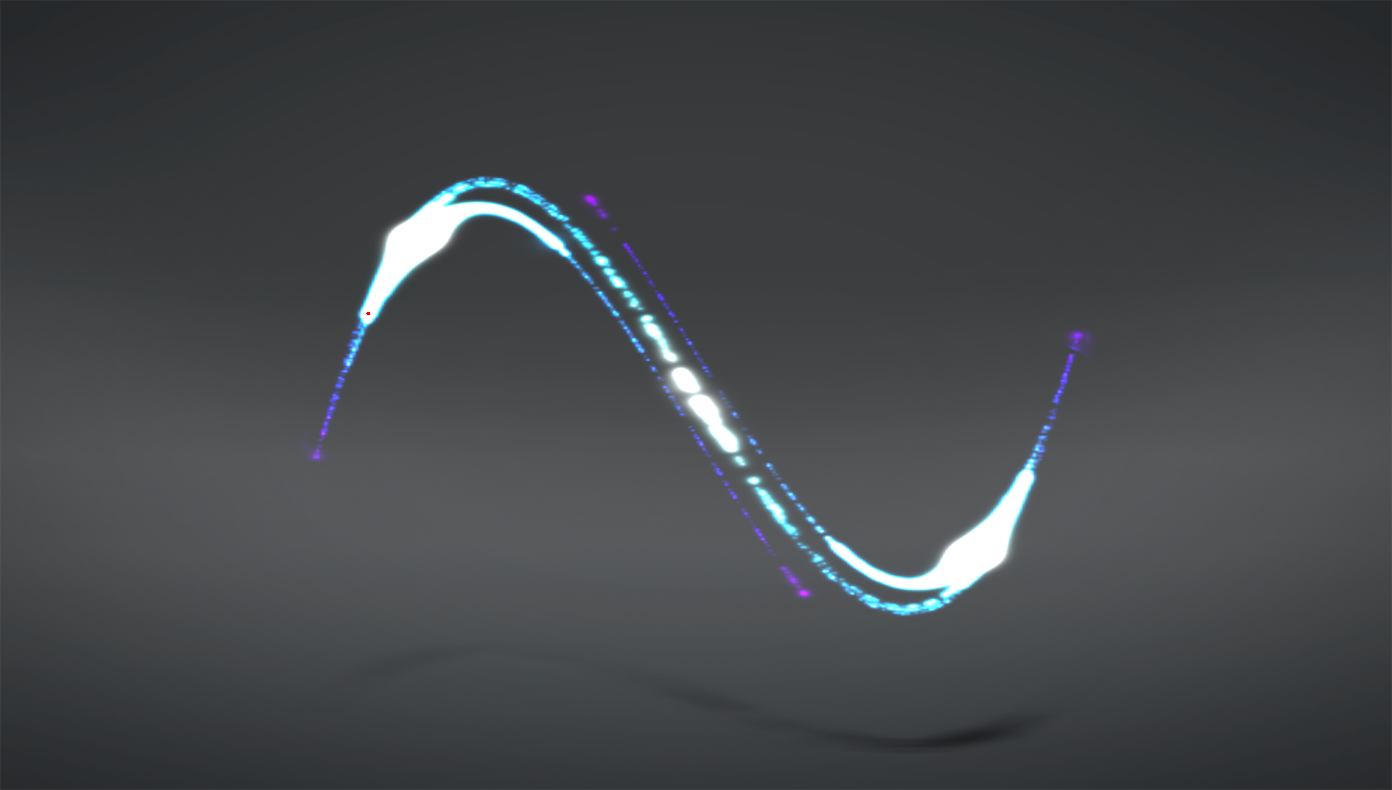
2D Strange Attractors | Chaos Theory
Strange attractors appear random but they are actually completely controlled by a set of variables and a starting position. They work by plugging the current position of a "brush" vector into a function with the set of variables. The brush is then moved to that new location and color is drawn in that spot. This continues for a specified amount of time. The resulting image is a stunning random looking design that's beauty wouldn't have been expected at first glance.
The randomness is the result of the principles of a field known as chaos theory. Namely, the fact that any minor change in any of the variables results in a nearly entirely different design. This makes the algorithm highly unpredictable thus rightfully earning the descriptor "chaotic."







2D Fractals | Fractals
Fractals such as the Mandelbrot seen in the top left example are a set of points within a space like a 2D plane that stay within the bounds of a particular set of rules. These rules typically come in the form of a complex equation that is iteratively and infinitely solved until either the point in that space (like a pixel on an image in this case) goes beyond a particular radius (magnitude of the point/vector) or fails to "escape" a set amount of iterations by staying within that radius for a set amount of time (max iterations). The pixel on the image that is plugged into this process then gets colored based on these bits of information.
Fractals are a stunning fact of nature that shows itself in everything from cell patterns in things like leaves to the borders of countries. They are self-similar meaning they replicate patterns of itself throughout the set. Additionally, you can theoretically zoom in endlessly on a particular point in the set and never hit the "bottom." These facts manifest themselves as beautiful repetitious patterns spiraling ever downward into a captivating abyss.
Fractals are useful for many things other than looks though. They can also be used for supplying computer graphics problems such as the rendering equation with a method for generating endless amounts of detail thus avoiding blurry or pixelated artifacts when users get too close to something.








Flow Fields | Generative Art
Flow fields (aka vector fields) are grid-like arrays of information that is used to direct objects in certain directions. They can be used in everything from pathfinding algorithms to simulating the flow of particles in a gassy medium. In this particular instance, I utilized a flow field to direct 2D particles around the screen and as they travel they are instructed to apply a paint stroke (but only under certain circumstances such as distance traveled). The resulting paint added up over generations of renderings creates the abstract paint stroke patterns as seen above.
In order to utilize a flow field, you must first decide upon how you are going to acquire the data necessary for directing particles. This can be done by a variety of means such as sin waves, image data, and even actual wind current information from various weather tracking services. In my particular case, I decided to use 2D Perlin Noise generated with an additional time variable so that the flow would change course seemingly randomly.
The flow field movement works by either plugging the coordinates of a particle into a function to get an output or matching the particle to the nearest data point via nearest neighbor search. Regardless of what type is used, the output of these operations are then turned into direction information and added onto a velocity vector tied to the particle. When the velocity is added onto the particle, the particle moves in the flow of the field.








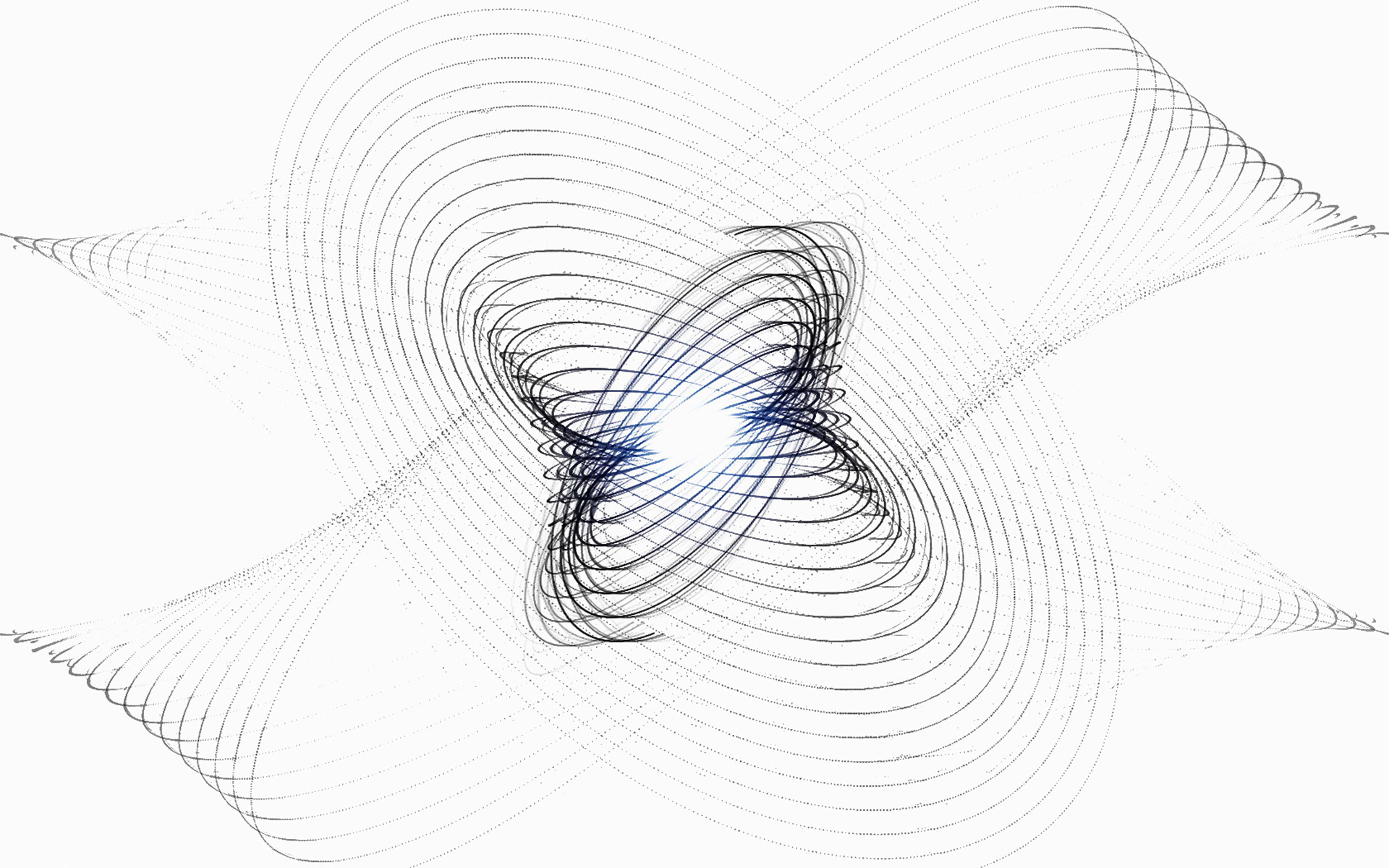
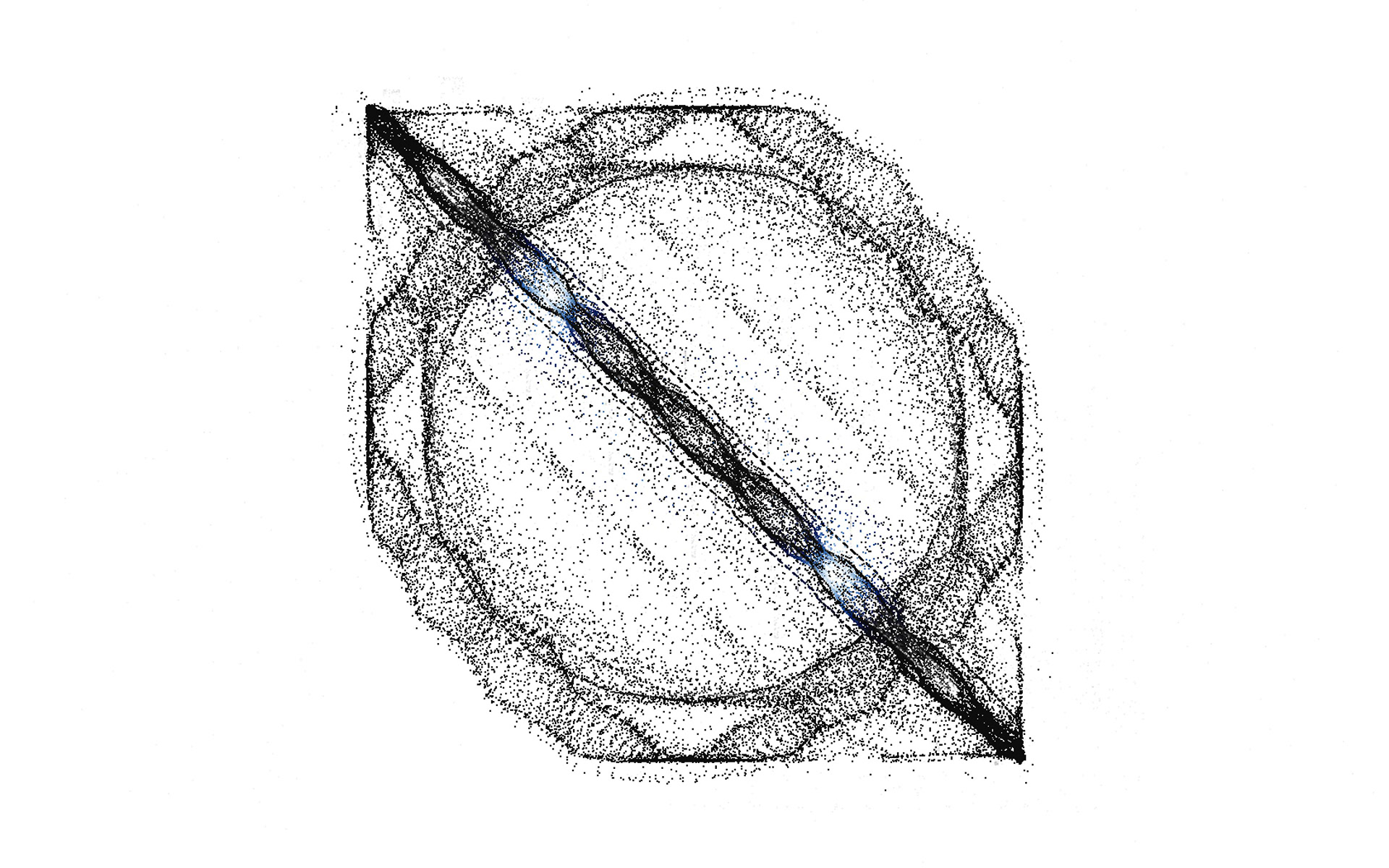


Iterated Function Systems | Generative Art
Iterated function systems (IFS for short) are generative (most of the time chaotic) algorithms that work by taking a population of particles, plugging their coordinates into a function, and overwriting these coordinates with new ones generated by the function. This may at first seem like a very simple process and it is, but the output of IFS algorithms can be very complex.
By taking the particles and rendering colored dots or lines each time they are ran through the function, we can visualize IFS algorithms as beautiful, sometimes repetitious and sometimes chaotic images.
There are many different IFS algorithms from attractors to fractals and even flow fields. In this particular case, I utilized an algorithm known as the chaos game to generate a wide variety of symmetric and chaotic designs. The chaos game works just like the general IFS algorithm discussed above but with the added step of randomly selecting a function from a set of functions each with their own probabilities (note that typical usage of the chaos game is by picking from vectors instead and moving between them using a linear interpolation function). Think of it as combining many different types of IFS into one to form a new one possibly with characteristics of each. The chaos game is great for procedural generation of content like video game foliage and its creative possibilities are infinite.


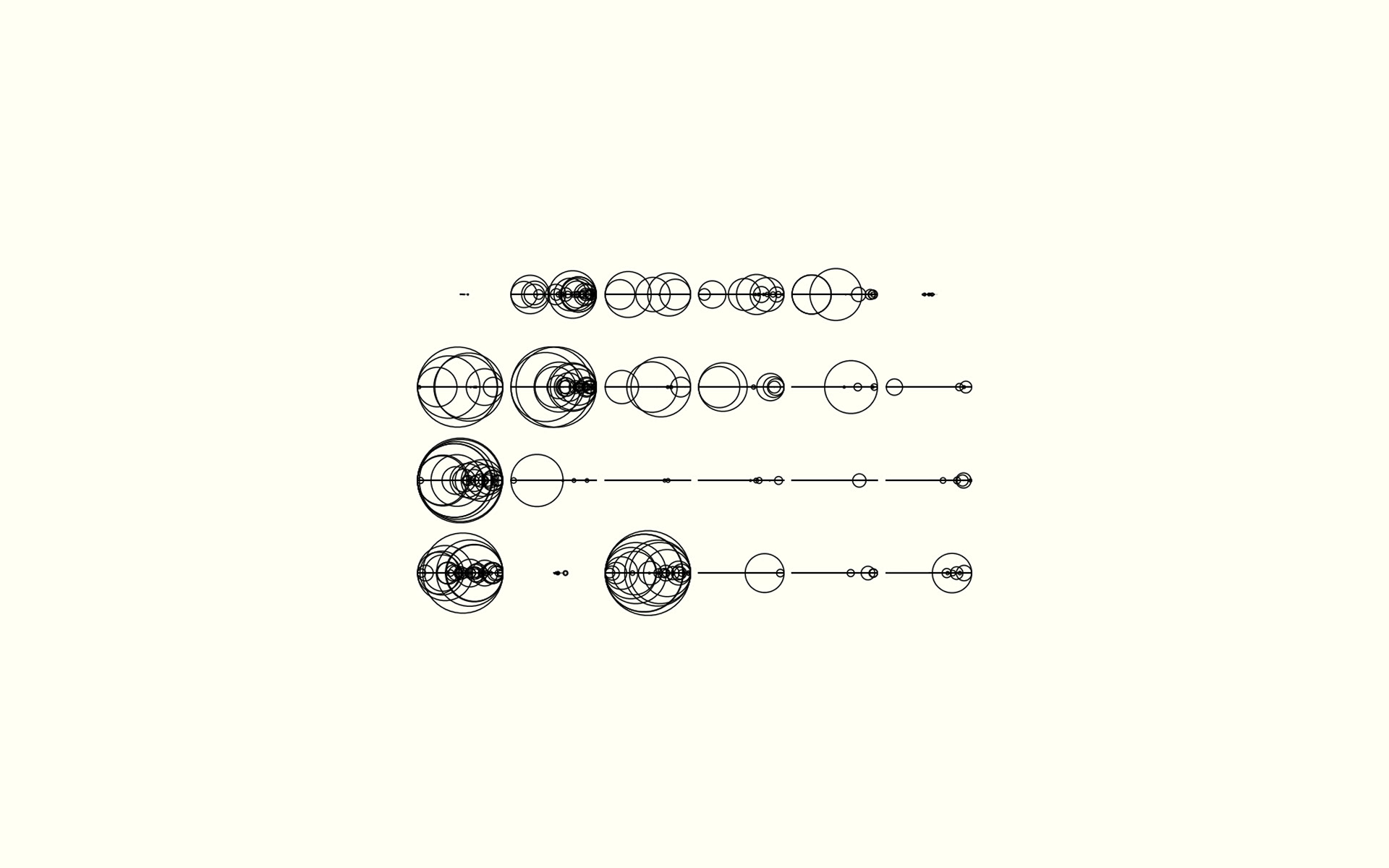
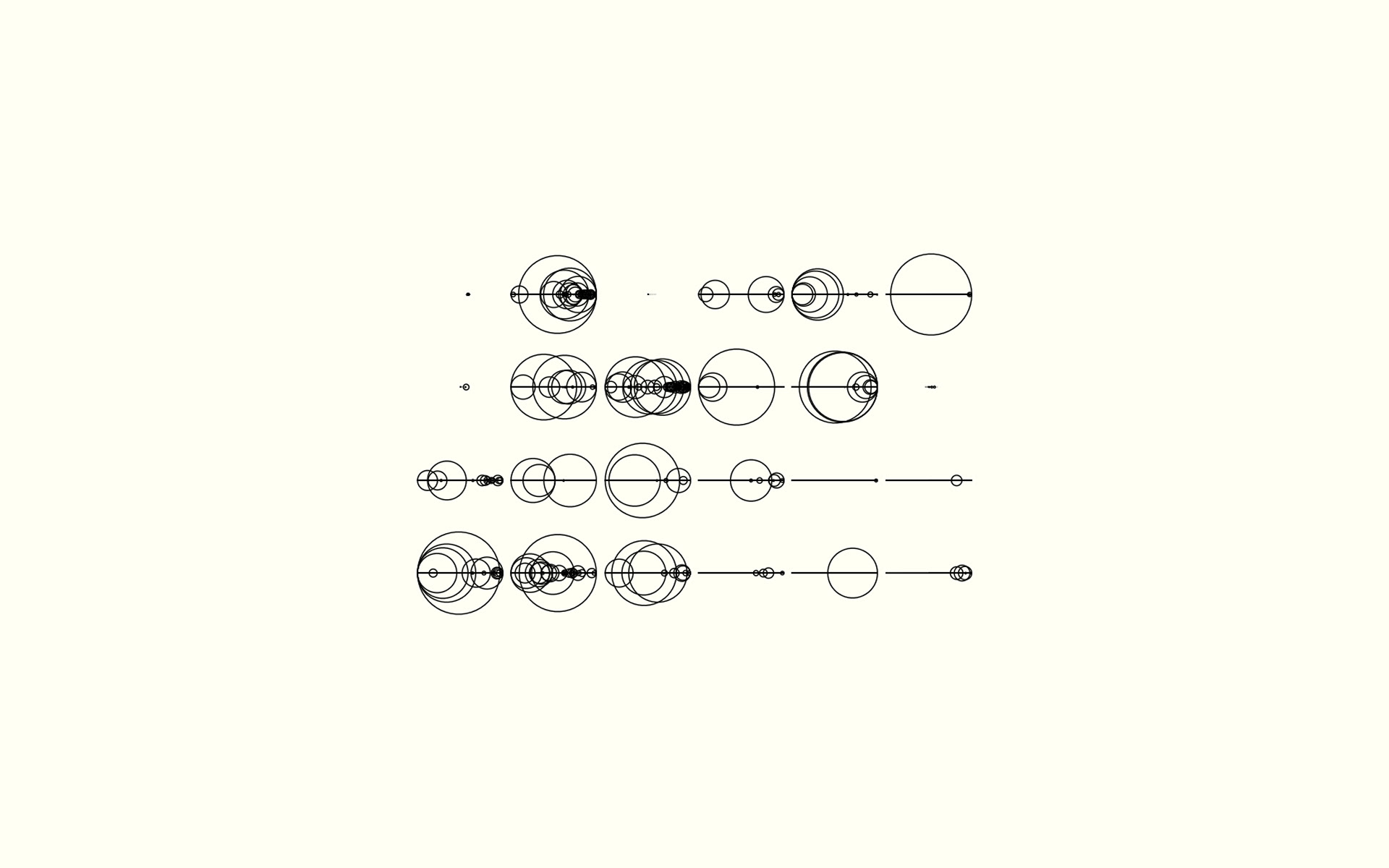

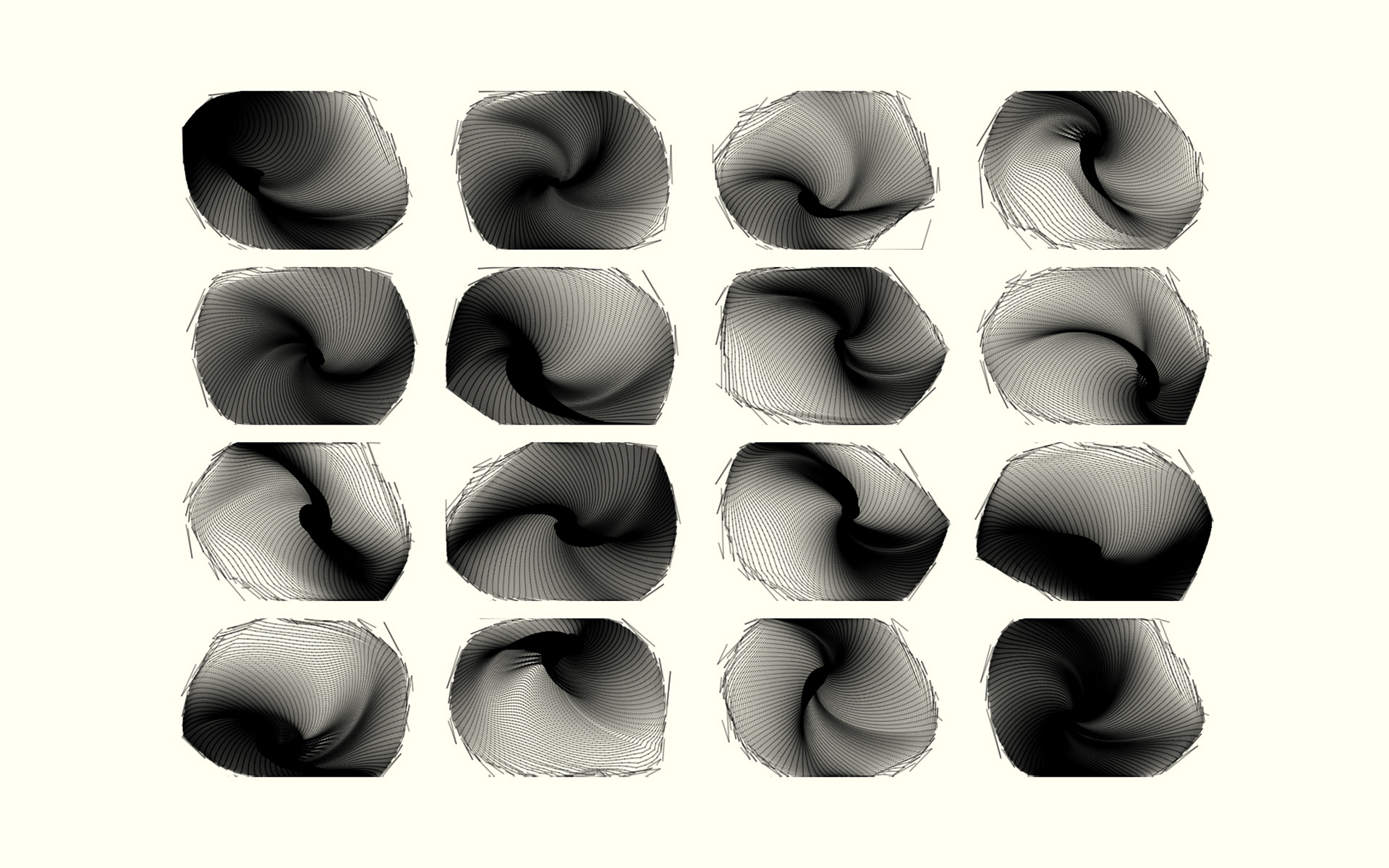
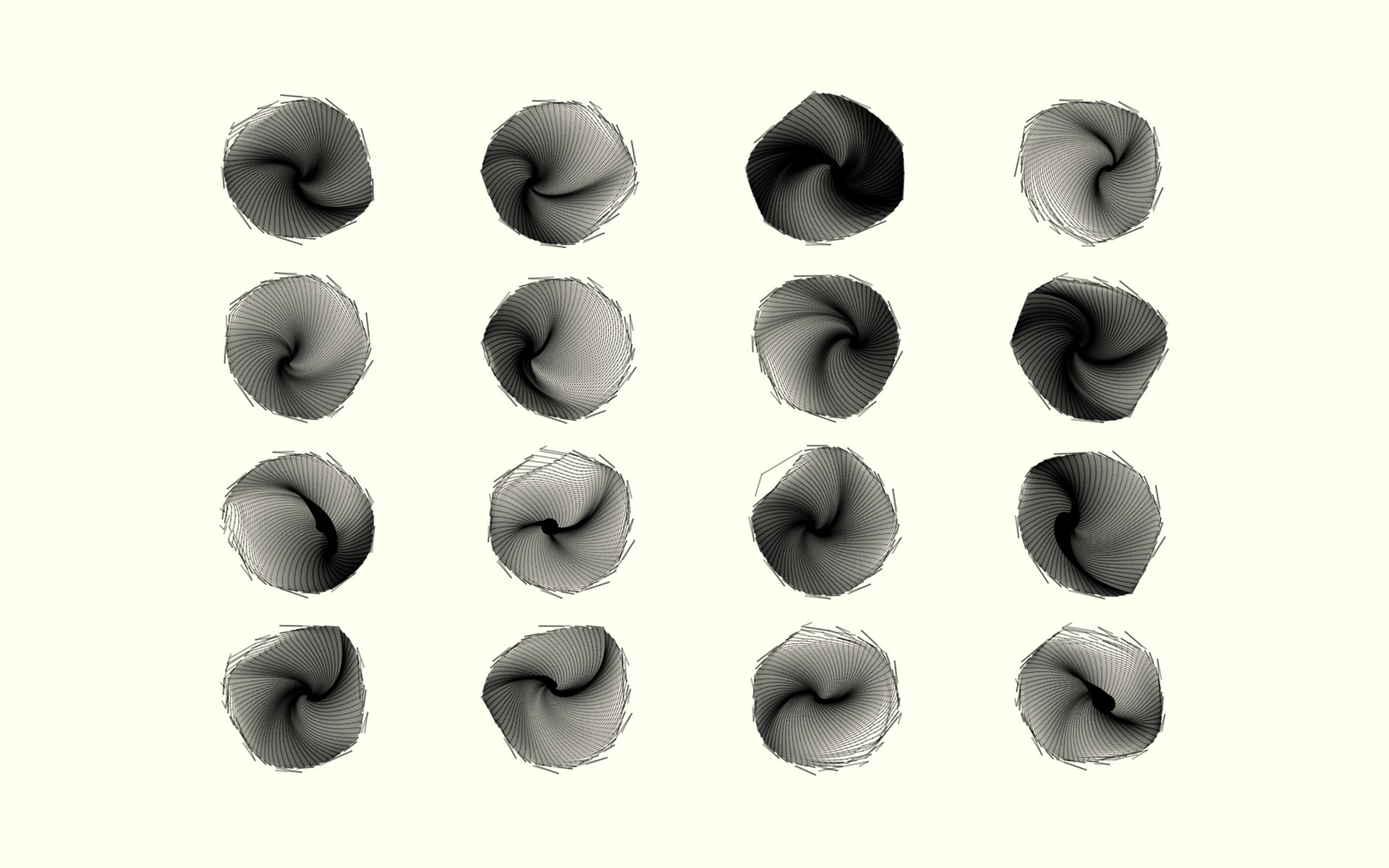
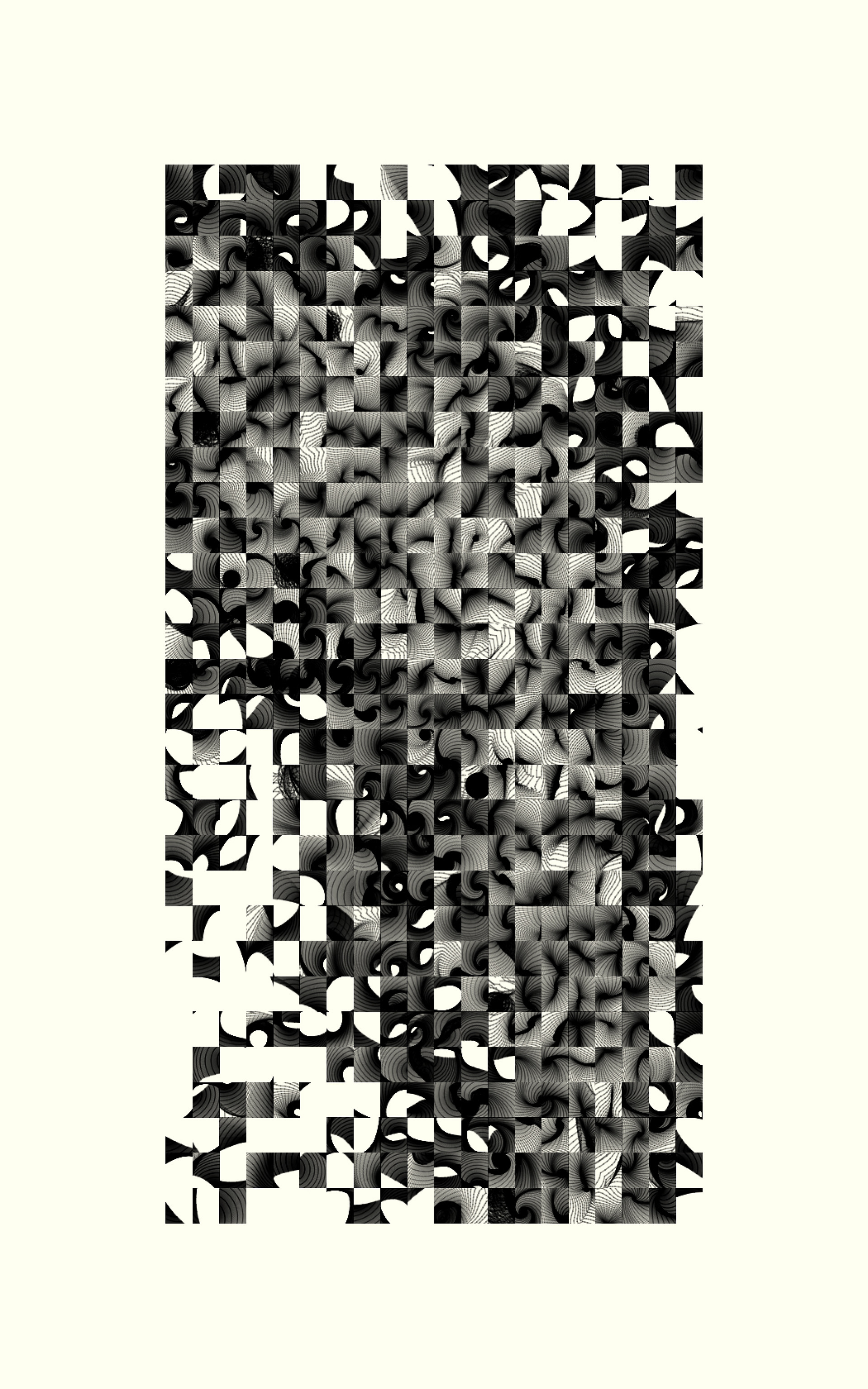





Uniform Expansive Shapes | Generative Art
This is a bit of a custom algorithm that incorporates elements of iterated function systems and physics. The results of these processes create a stunning variety of complex and simplistic designs that can then be juxtaposed in a grid structure for further artistic effect.
The algorithm works by starting with a polygon in some arbitrary form (random, circle, a picture etc). It then goes through a manipulation and a rendering step for each of many iterations. The results seen above are a result of all these rendering steps composed on top of one another.
In the manipulation step, each point in the polygon is manipulated according to some forces exerted on them by things like how close they are to the mean of the polygon and how close they are to their neighboring points. These forces drive the whole polygon in a way that appears as if the polygon is bouncing around (like a soft-body physical object). Next, the line segments formed by each pair of points (in clockwise order) are split into two new line segments with a new point added in the middle only when the length of the original line segment is long enough. This causes the polygon to expand and form interesting procedural shapes.
In the rendering step, random rendering styles (like shape, fill mode, size, opacity and more) are selected based on some probability and applied on top of a buffer (merging with what has already been drawn). Other restrictions are placed on the different styles (such as circles having a radius equal to the length of each line segment) to create interesting relationships between these visual elements.
For even more of a fascinating artistic effect, a number of different images are rendered using this algorithm and then placed side by side in a grid structure for uniformity among non-uniform art. Don't worry, the background is just colored like paper.
Expansive Shape | Generative Art
This particular piece is a result of the Expansive Shapes algorithm detailed above but with a specific set of parameters that result in chaotic behavior. From this, an animation is born that appears at first to be pure chaos but when time goes on, patterns begin to emerge and slow down. Bigger and bigger triangles and other geometric shapes begin to form out of smaller ones. The overall image appears to be like an animated modern art piece.
Rendering the polygons from the original algorithm above is done by determining the direction each point is traveling and applying Lambertian reflectance based off of this and a pre-defined light direction. The results were unexpected yet most interesting!
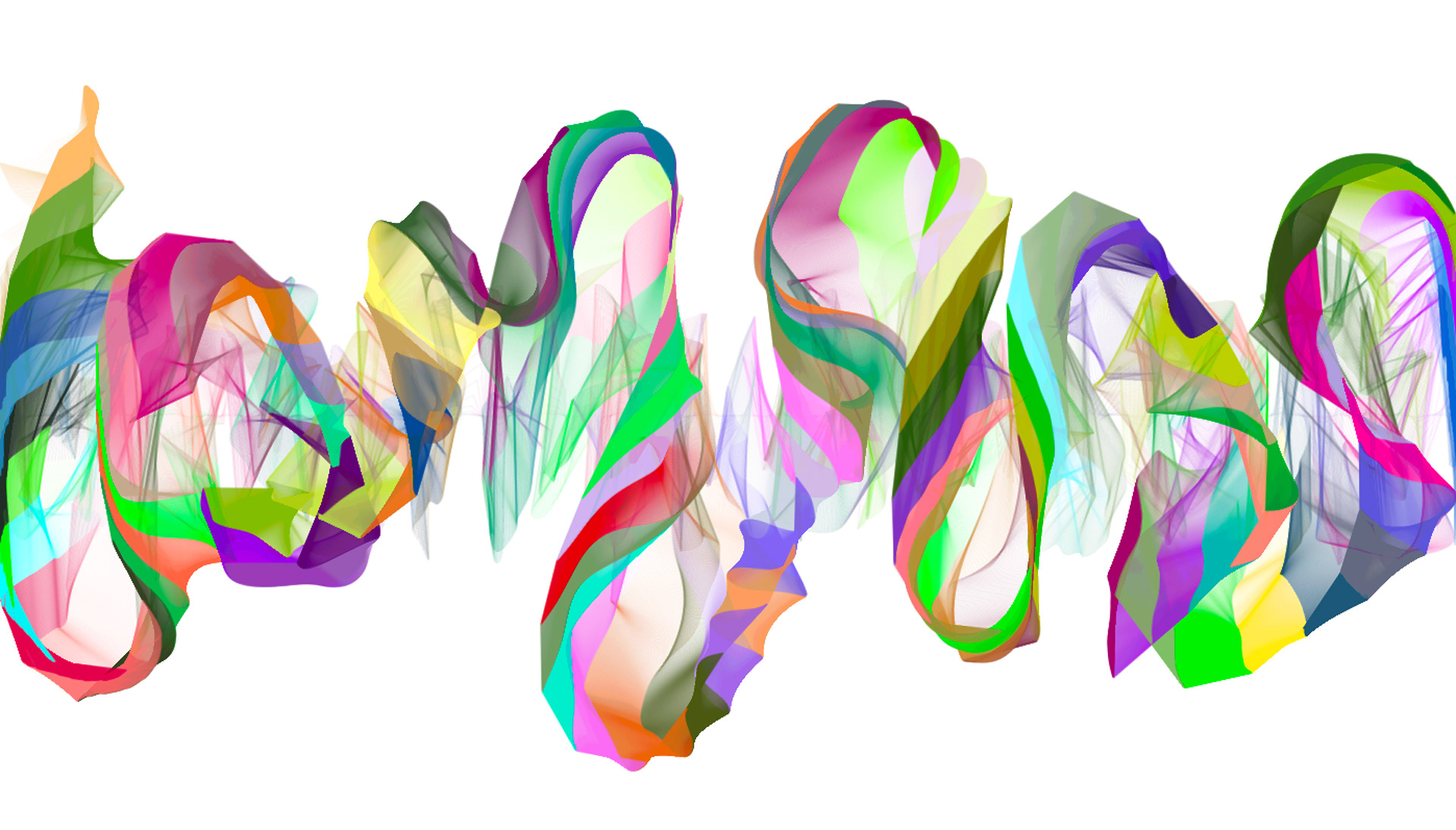


Processing Physics Whip | Generative Art
These pieces were created in Processing using a series of particles connected via spring-dampers. Spring-dampers are links between two points that apply push-pull forces on each point until a particular distance is achieved (aka resting distance). The result is what it looks like to pull a spring in real life. The way in which the spring-dampers are connected range from horizontal open-ended lines to loops. Chaotic behavior is then achieved by randomly adjusting the resting distances of each spring-damper.
When rendering, triangles are drawn between each particle and their left and right neighbors. Color is either presented in greyscale, randomly selected, or determined by distance traveled. Transparency is also applied so that gradation is achieved. The results are quite interesting!

